RIPAL: Responsive and Intuitive Parsing for the Analysis of Language

Background

We've now seen how we can derive strings that belong to some language using a context-free grammar. One of the next questions you might ask about such a derivation is "What does this mean?"

What is a parse tree?

Definition

A parse tree is a structure that illustrates the structure of a string as part of a language. In particular, a parse tree illustrates, in a recursive structure, what a nonterminal symbol produces within a particular string's derivation via the rules in a grammar.

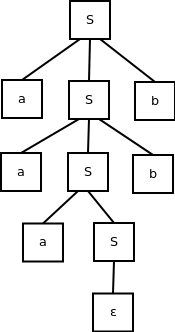
Example

Example

Let's say we are examining the language specified by the following context-free grammar:

Example derivation:

SENTENCE → SUBJECT VERB OBJECT. (via rule 1) → John VERB OBJECT. (via rule 2) → John threw OBJECT. (via rule 3) → John threw QUALIFIEDOBJECT. (via rule 4) → John threw the ADJECTIVE puck. (via rule 6) → John threw the heavy puck. (via rule 7)

Based on this, we know that the sentence "John threw the heavy puck." is part of our language. But what does it mean?

The following parse tree represents our string derivation:

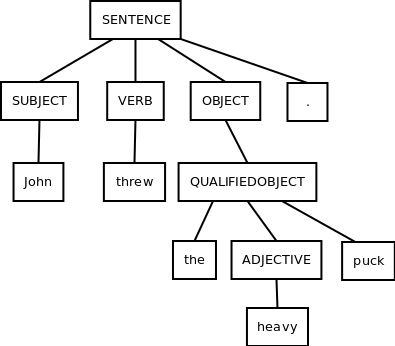
Parse tree for the string 'John threw the heavy puck.' SENTENCE is at the top of the parse tree. On the second level, SENTENCE becomes 4 symbols: SUBJECT, VERB, OBJECT and PERIOD. On the third level, SUBJECT becomes John, VERB becomes threw and OBJECT becomes QUALIFIEDOBJECT. On the fourth level, QUALIFIEDOBJECT becomes 3 symbols: the, ADJECTIVE and puck. On the fifth level, ADJECTIVE becomes heavy.

We can learn the following from seeing a parse tree for a string (without requiring any external information):

We know that our string is part of our language from the presence of the parse tree
We can determine what the input string is by reading the terminal nodes from the tree
1. A simple left-to-right read of the nodes with no children produces the input string - in this case, "John threw the heavy puck."
We can determine the productions used to derive our string by reading the nonterminal nodes from the tree and observing their direct child nodes
1. For example, we can tell that the production "SENTENCE → SUBJECT VERB OBJECT." is used in this derivation by observing the top nonterminal node and its children
We can determine, structurally, what conceptual part of the language structure a nonterminal, terminal or ε node belongs to
1. For example, we know that the terminal "puck" belongs to a qualified object and that the terminal "heavy" is an adjective that belong to a qualified object

Removing string ambiguity with a parse tree

Example

Let's say we have the following context-free grammar:

S → aSb
S → aS
S → ε

By inspection, it's not to hard to understand that this CFG specifies the following language:

L = {a^{n + k}bⁿ | n, k >= 0}

Informally, this language contains the empty string, plus some number of as following by some number of bs where there are at least as many as as bs.

Deriving a string:

S → aSb (via rule 1) → aaSbb (via rule 1) → aaaSbb (via rule 2) → aaabb (via rule 3)

From this derivation, we know that aaabb ∈ L. The corresponding parse tree is:

Parse tree for the string 'aaabb'. S is as the top of the parse tree. On the second and third levels, S becomes 3 symbols: a, S and b. On the fourth level, S becomes 2 symbols: a and S. On the fifth level, S becomes ε.

From this parse tree, we can tell that, in our derivation, we chose to introduce the unbalanced "a" symbol deep within the structure of our derivation. It can use used here to remove ambiguity from the meaning of our input string.

Conclusion

We can use parse trees to ilustrate the structure and hence the meaning of an input string within our language.