RIPAL: Responsive and Intuitive Parsing for the Analysis of Language

Pages

Converting an NFA to a DFA

Background

We've seen the process of converting and ε-NFA to an NFA. This process will be extremely helpful in converting regular expressions into a state machine that's easy to use. However, NFAs may still have multiple transitions for the same input symbol from the same state, which can still make the recognition process difficult. In this section, we'll demonstrate how to convert an NFA into a DFA in order to provide a simpler recognition mechanism.

Example

Example

The following NFA contains multiple transitions for the same input symbol from the same state:

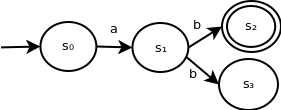
NFA with multiple transitions for the same state and symbol. This NFA contains 4 states - s0, s1, s2 and s3. s0 transitions to s1 on input symbol a. s1 transitions to s2 and s3 on input symbol b. s2 is accepting.

This NFA recognizes the language L = {ab}. When parsing the string ab, after we encounter symbol b in state s1, we can choose to transition to state s2 or s3. Since we are only looking for a single path to an accepting state, we would choose to transition to s2 and accept the string.

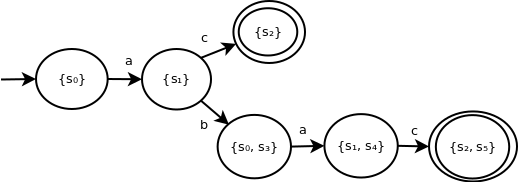
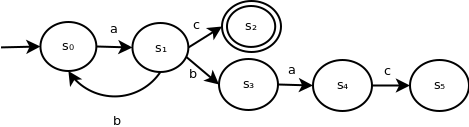
As a result, this NFA is equivalent to the following DFA:

Simplified DFA. This DFA contains 3 states - s0, s1 and s2. s0 transitions to s1 on input symbol a. s1 transitions to s2 on input symbol b. s2 is accepting.

More complex example

Example

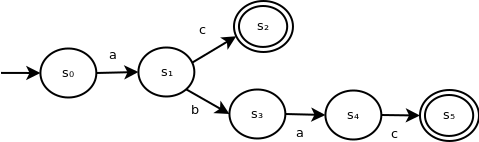
The following is an example of an NFA that is significantly more complex:

Complex NFA with multiple transitions for the same symbol and state. This NFA contains 6 states - s0 through s5. s0 transitions to s1 on input symbol a. s1 transitions to s0 and s3 on input symbol b. s1 transitions to s2 on input symbol c. s3 transitions to s4 on input symbol a. s4 transitions to s5 on input symbol c. s2 is accepting.

Here, it's less clear how to reduce this to a DFA.

Now, consider the transitions from s1 for input symbol b. The possible set of next states is: {s0, s3}.

Since we only need to find a single path for a certain input string to an accepting state, we would continue the process of considering the set of all possible next states as we iterate through the input string.

For example, if we process input characters a then b, our possible set of states is {s0, s3}. On subsequent input symbol a, the next set of possible states is: {s1, s4}.

Reduction process

To outline the reduction process, for our set of states S, we must consider the power set of S.

Defintion

Given our set of states

S = {s0, s1, ..., sn - 1}

The power set of S is defined as:

P(S) = {{}, {s0}, ..., {sn - 1}, {s0, s1}, {s0, s2}, ..., {sn - 2, sn - 1}, {s0, s1, s2}, ..., {s1, s2, ..., sn - 1}}

Informally, the power set of S is the set containg all possible subsets of S.

Since, as illustated above, we need to consider combinations of possible states, we will construct a new set of states in our DFA which maps to some combination of states from our DFA. Specifically, these combinations map to some element of the power set of S, P(S).

Our DFA's start state corresponds to the element {s0} from P(S), since this is where our parsing process starts.

Next, we must consider the process of working through the NFA to add additional states to our DFA.

We will consider a DFA state which represents some set of states from the original NFA. For each input symbol corresponding to a transition from any of the original DFA states, track all states from the DFA that would be transitioned to for that input symbol. Then, we create a new DFA state corresponding to that set of NFA states (or reuse the DFA state corresponding to that combination if one exists). Then, we can add a transition to it from the previous state.

We set our new DFA state to accepting if at least one of the NFA states it was derived from is accepting.

More complex example reduced

Example

Following the instructions above, our complex NFA can can be reduced to the following DFA:

Simplified DFA. This DFA contains 6 states, each of which represents some set of states from the DFA. State with set s0 transitions to state with set s1 on input symbol a. State with set s1 transitions to state with set s2 on input symbol c. State with set s1 transitions to state with set s0, s3 on input symbol b. State with set s0, s3 transitions to state with set s1, s4 on input symbol a. State with set s1, s4 transitions to state with set s2, s5 on input symbol c. All new states containing s2 are accepting.

Finally, we can re-label the states as follows:

Simplified DFA relabelled This dfa contains 6 states - s0 through s5. s0 transitions to s1 in input symbol a. s1 transitions to s2 on input symbol c. s1 transitions to s3 on input symbol b. s3 transitions to s4 on input symbol a. s4 transitions to s5 on input symbol c. s2 and s5 are accepting.

Note that the two states whose state set from the NFA contain s2 are marked as final states.

Conclusion

In conclusion, we now have a process to convert an NFA to a DFA. Using Thompsons's construction along with the ε-NFA to NFA conversion process, we can now convert regular expressions into NFAs for straightforward recognition.

GitHub Repository: https://github.com/bprollinson/ripal

Copyright © 2017 Brendan Rollinson-Lorimer