RIPAL: Responsive and Intuitive Parsing for the Analysis of Language

Background

We've seen a method for constructing ε-NFAs from regular expressions. However, using an ε-NFA to recognize a string as part of a language is tricky. We will look at a method to convert ε-NFAs to NFAs to simplify the recognition process.

Removing ε transitions

Example

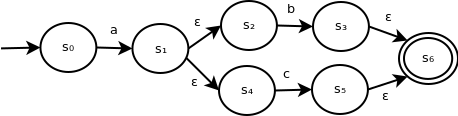
Observe the following ε-NFA:

ε-NFA with epsilon transition before character transition. This ε-NFA contains 3 states - s0, s1 and s2. s0 transitions to s1 on input symbol ε s1 transitions to s2 on input symbol a. s2 is accepting.

This recognizes the string "a". Because the ε transition doesn't consume an input symbol, it can be simplified to the following:

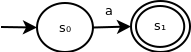
Simplified NFA. This NFA contains 2 states - s0 and s1. s0 transitions to s1 on input symbol a. s1 is accepting.

Note that we've done some state relabelling for readability after s₁ was eliminated from the original machine.

Similarly, the following ε-NFA recognizes the same language:

ε-NFA with multiple epsilon transitions before character transition. This ε-NFA contains 4 states - s0, s1, s2 and s3. s0 transitions to s1 on input symbol ε s1 transitions to s2 on input symbol ε s2 transitions to s3 on input symbol a. s3 is accepting.

When we are converting an ε-NFA into an NFA, we may encounter a sequence of ε transitions linking state s₀ through s_{n - 2}, followed by a transition with input symbol σ from state s_{n - 2} to state s_{n - 1}. We can replace it with a two-state construction of state s₀ transitioning to s_{n - 1} on input symbol σ.

This allows us to eliminate leading ε transitions and unnecessary states, simplifying our automaton without affecting the set of strings it accepts.

Making states accepting

Example

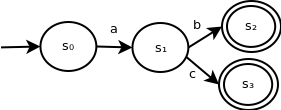
Observe the following ε-NFA:

ε-NFA with epsilon transition before accepting state. This ε-NFA contains 3 states - s0, s1 and s2. s0 transitions to s1 on input symbol a. s1 transitions to s2 on input symbol ε. s2 is accepting.

This recognizes the string "a". Because the ε transition doesn't consume an input symbol, it can be simplified to the following:

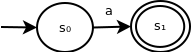
Similarly, the following ε-NFA recognizes the same language:

ε-NFA with multiple epsilon transitions before accepting state. This ε-NFA contains 4 states - s0, s1, s2 and s3. s0 transitions to s1 on input symbol a. s1 transitions to s2 on input symbol ε. s2 transitions to s3 on input symbol ε. s3 is accepting.

When we are converting an ε-NFA into an NFA, we may encounter a sequence of ε transitions linking state s₁ through s_{n - 1} following a transition with input symbol σ from state s₀ to state s₁. We can replace it with a two-state construction of state s₀ transitioning to s_{n - 1} with input symbol σ. If s_{n - 1} was accepting in the initial construction, it will be in the new construction.

This allows us to remove trailing states without affecting the set of strings accepted by the automaton.

Summary

Following the above rules, we can convert an ε-NFA into an NFA, removing all ε transitions. However, we may still have states with multiple transitions corresponding to the same symbol.

More complex example

Example

Complex ε-NFA with multiple epsilon transitions leading to character transitions and accepting states. This ε-NFA contains 7 states - s0 through s6. s0 transitions to s1 on input symbol a. s1 transitions to s2 and s4 on input symbol ε s2 transitions to s3 on input symbol b. s4 transitions to s5 on input symbol c. s3 and s5 transition to s6 on input symbol ε s6 is accepting.

Using the same rules as above, this can be reduced to the following NFA (which happens to, by chance, also be a DFA):

Simplified NFA. This NFA contains 4 states - s0, s1, s2 and s3. s0 transitions to s1 on input sybmol a. s1 transitions to s2 on input symbol b. s1 transitions to s3 on input symbol c. s2 and s3 are accepting.

RIPAL: Responsive and Intuitive Parsing for the Analysis of Language

Pages

Converting an ε-NFA to an NFA

Background

Removing ε transitions

Making states accepting

Summary

More complex example